Grundschaltungen
Anhand der folgenden Grundschaltungen werden die Beziehungen zwischen Spannung, Strom und Widerstand weiter vertieft. Das Ziel ist, die bisherigen Erkenntnisse zu bestätigen und um weitere Gesetzmäßigkeiten zu ergänzen. Wobei die Grundlage für die Zusammenhänge nach wie vor das Ohmsche-Gesetz darstellt. Zur Auffrischung siehe Blogbeitrag Das Ohmsche-Gesetz
Bei Betriebsmitteln (Spannungsquellen bzw. Erzeugern und Verbrauchern), die jeweils nur zwei Anschlusspunkte besitzen, verwendet der Fachmann auch den Begriff „Zweipole„. Zweipole vom Typ Verbraucher, die in den folgenden Schaltungen vereinfacht als Widerstände dargestellt werden, sind z.B. Lampen, Spulen von Relais oder Pneumatikventilen, Strom- und Spannungsmesser, passive Bauteile (Widerstände, Kondensatoren, Spulen, Dioden), Elektromotoren usw.. Praktischerweise können vereinfacht alle Zweipole als Widerstand dargestellt werden, da die Steckdose ja nicht weis, was angeschlossen wird. Sie stellt nur die geforderte Spannung zur Verfügung und der Stromfluss stellt sich dann automatisch, aufgrund des „Widerstandes“ den der Zweipol darstellt, ein.
Reihenschaltung von Widerständen
Von einer Reihenschaltung spricht man, wenn der Strom nacheinander durch die angeschlossenen Verbraucher fließt. Oft wird auch der Begriff Serienschaltung verwendet. Das heißt, die Stromstärke ist an jeder Stelle des Stromkreises gleich groß.
In einer Reihenschaltung gilt: I = konstant
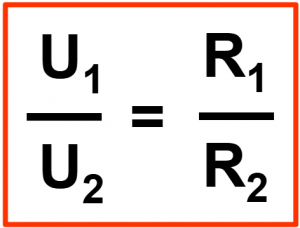
In einer Reihenschaltung verhalten sich die abfallenden Spannungen an den Verbrauchern wie die Widerstände. Dies bedeutet, am größeren Widerstand fällt auch die größere Spannung ab.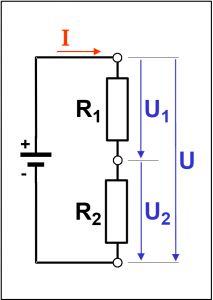
Die Gesamtspannung (U) ist so groß, wie die Summe aller Teilspannungen (U1, U2, …).
Nachdem in allen Widerständen der gleiche Strom fließt, folgt daraus, dass die Summe aller Teilwiderstände gleich dem Gesamtwiderstand ist 
.
Dieser Gesamtwiderstand R wird auch als Ersatzwiderstand bezeichnet und mit RG dargestellt. Da bei der Betrachtung der Spannungsabfälle auch die Erzeugerspannung (Uq) berücksichtigt werden muss, ergibt sich folgender Zusammenhang:
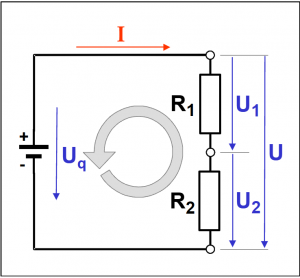Im gezeigten Schaltbild erkennt man, dass es sich um einen
geschlossenen Kreislauf handelt, eine „Masche„.
Somit gilt die zweite kirchhoffsche Regel, die „Maschenregel„.
In einer Masche ist die Summe der Quellenspannungen
und der Teilspannungen an den Verbrauchern gleich null!
Beachte, bei vorgegebener Zählrichtung, die Richtung der Spannungspfeile!
Uq – U2 – U1 = 0 oder Uq = U1 + U2 oder Uq – U = 0 oder Uq = U
Parallelschaltung von Widerständen
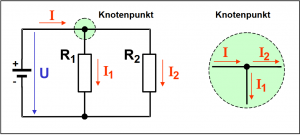
Von einer Parallelschaltung spricht man, wenn die Spannung an jedem Verbraucher gleich groß ist. Die Widerstände sind nebeneinander angeordnet. Das heißt, die Spannung an den Verbrauchern ist gleich, aber der Strom teilt sich mindestens an einer Stelle auf (Stromverzweigung).
In einer Parallelschaltung gilt: U = konstant
In einer Parallelschaltung teilt sich der Strom auf die einzelnen Verbraucher in Teilströme auf. Die Teilströme verhalten sich umgekehrt wie die zugehörigen Widerstandswerte. Dies bedeutet, durch den größeren Widerstand fließt auch der kleinere Strom.
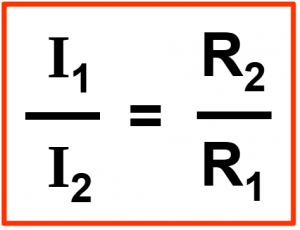
Der Gesamtstrom (I) ist damit so groß, wie die Summe () aller Teilströme (I1, I2, …).
Die Verhältnisse in einem Knotenpunkt beschreibt die erste kirchhoffsche Regel, die sogenannte. „Knotenpunktregel„.
In einem Knotenpunkt ist die Summe der zufließenden Ströme genauso groß,
wie die Summe der abfließenden Ströme
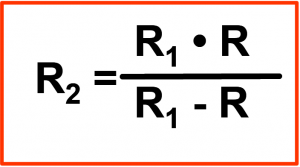
Die Berechnung des Gesamtwiderstandes ist bei der Parallelschaltung nicht ganz so einfach wie zuvor bei der Reihenschaltung. Aber auch hier gilt nach wie vor das „Ohmsche Gesetz„. Bei der Parallelschaltung von nur zwei Widerständen gilt die Formel:
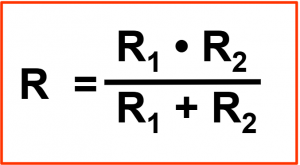
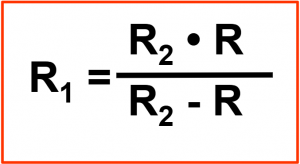
Nachdem der Leitwert dem Kehrwert des Widerstandes entspricht, besteht auch die Möglichkeit den Ersatzwiderstand (Gesamtwiderstand) bei einer Parallelschaltung über die Leitwertaddition zu errechnen. Dies ist besonders bei einer Parallelschaltung von mehr als zwei Widerständen besonders hilfreich.
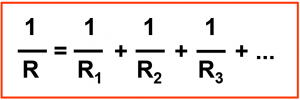In einer Parallelschaltung ist der Ersatzleitwert gleich der Summe der Einzelleitwerte.
Achtung: Das Ergebnis ist nicht der Ersatzwiderstand, sondern der Ersatzleitwert. Um den Widerstandswert zu ermitteln, ist der Kehrwert des Ersatzleitwertes zu berechnen.
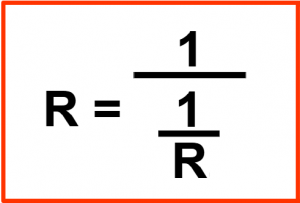
Merke: In einer Parallelschaltung ist der Ersatzwiderstand kleiner als der kleinste Einzelwiderstand.
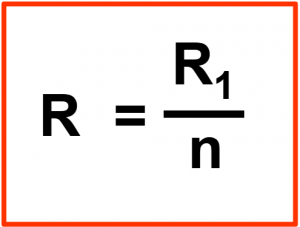
Besteht die mehrfache Parallelschaltung aus gleichen Widerstandswerten (Anzahl = n), ergibt sich eine Vereinfachung:
Gemischte Schaltungen von Widerständen
Gemischte Schaltungen bestehen aus einer Kombination mehrerer Reihen- und Parallelschaltungen. Was in der Praxis wesentlich häufiger vorkommt als eine reine Reihen- oder Parallelschaltung. Zur Berechnung von gemischten Schaltungen ist es notwendig, für die einzelnen Schaltungsteile die jeweiligen Ersatzwiderstände zu errechnen. Dies wird so lange wiederholt, bis nur noch der Gesamtwiderstand übrig bleibt.
Dieses Verständnis der Schaltungsberechnungen ist Grundvoraussetzung, um im Bedarfsfall geeignete Vorwiderstände für Verbraucher, für elektronische Bauteile oder für Messbereichserweiterungen zu berechnen.
Eine besondere Stellung im Zusammenhang mit gemischten Schaltungen nimmt der Spannungsteiler ein. Aber dem Spannungsteiler widmen wir einen eigenen Blogbeitrag.
Beispiel 1:
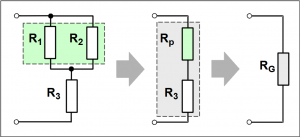
Zuerst wird der Ersatzwiderstand Rp aus der Parallelschaltung von R1 und R2 berechnet. Die anschließende Berechnung der Reihenschaltung aus Rp und R3 ergibt den Gesamtwiderstand RG der Schaltung. Hierzu werden 2 Rechenschritte benötigt.
Beispiel 2:
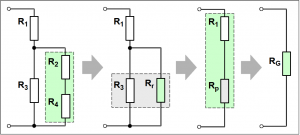
Zuerst wird der Ersatzwiderstand Rr aus der Reihenschaltung R2 und R4 berechnet. Danach erfolgt die Berechnung der Parallelschaltung (Rp) von R3 und Rr . Die anschließende Addition der Widerstandswerte von R1 und Rp (Reihenschaltung) ergibt den Gesamtwiderstand RG der Schaltung. Hierzu werden 3 Rechenschritte benötigt.
Beispiel 3:
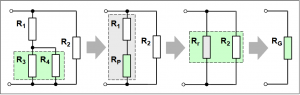
Zuerst wird der Ersatzwiderstand Rp aus der Parallelschaltung von R3 und R4 errechnet. Danach erfolgt durch Addition die Berechnung der Reihenschaltung (Rr) von R1 und Rp. Die anschließende Berechnung der Parallelschaltung von Rr und R2 (Reihenschaltung) ergibt den Gesamtwiderstand RG der Schaltung. Hierzu werden 3 Rechenschritte benötigt.
Erkenntnis:
Bei der Zusammenfassung der einzelnen Widerstandswerte als Reihen- bzw. Parallelschaltung ist darauf zu achten, dass nur solche Widerstände zusammengefasst werden, bei denen die gleichen Bedingungen herrschen. Das heißt gleiche Spannung oder gleicher Strom.
Es können nur solche Widerstandswerte zusammengefasst werden,
bei denen die gleichen Spannungs- oder Stromwerte vorliegen.
Resümee:
Haushaltsgeräte bzw. Verbraucher können nicht in Reihenschaltung oder Gemischter-Schaltung betrieben werden, weil sie sonst an unterschiedlichen Spannungen anliegen. Haushaltsgeräte bzw. Verbraucher werden immer in Parallelschaltung betrieben. Für ihre sichere Funktion benötigen alle Betriebsmittel die gleiche Spannung (230 VAC). Somit müssen auch Steckdosen immer parallel angeschlossen werden!
