Was ist Blindleistung bzw. was sind Blindanteile?
Erforderliches Grundlagenwissen:
- Ohmsches Gesetz
- Elektrische Leistung
- Widerstand
- Induktionsgesetz
- Spule bzw. Induktivität
- Kondensator bzw. Kapazität
Ohmscher Widerstand
Blindanteile entstehen nur beim Zusammentreffen von
Wechselspannung mit Induktivitäten und / oder Kapazitäten!
Wird ein ohmscher Widerstand an eine Wechselspannung (AC) angeschlossen, stellt sich in Abhängigkeit der Spannung und des Widerstandswertes ein entsprechender Strom ein (I = U / R). Schaut man sich jetzt den zeitlichen Verlauf von Spannung und Strom an, erkennt man, dass beide dem gleichen Kurvenverlauf folgen. Sie erreichen zum gleichen Zeitpunkt ihren Maximalwert und die Nulllinie. Man sagt, sie sind in Phase bzw. es gibt keine Phasenverschiebung zwischen Strom und Spannung. Somit ist es kein Problem die elektrische Leistung zu berechnen (P = U x I).
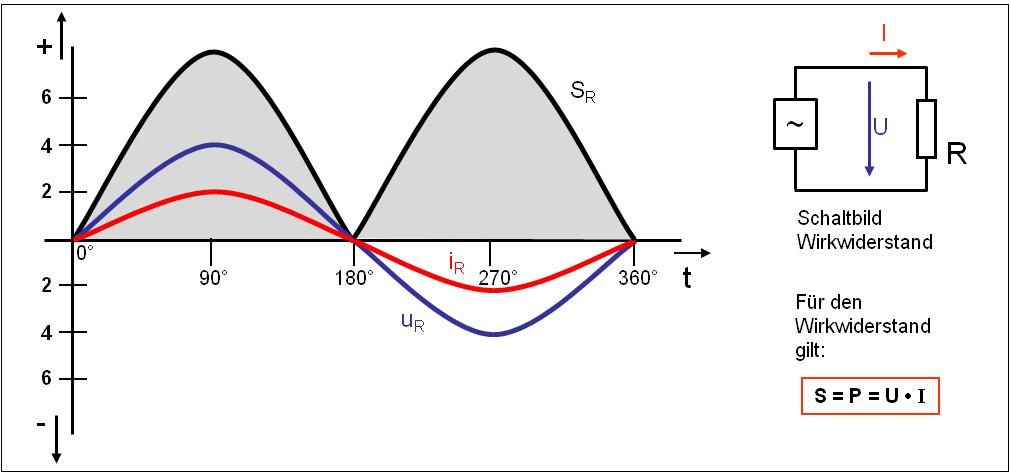
Prinzipiell gilt für die Berechnung der Scheinleistung die Formel 
, für die Berechnung der Wirkleistung die Formel 
. Da beim Wirkwiderstand Strom und Spannung in „Phase“ sind, also keine Verschiebung bzw. zeitlicher Versatz vorhanden ist, ist der Wirkleistungsfaktor cos phi (Verhältnis von P/S) mit 1 zu rechnen (cos phi = 00). Daraus folgt. Scheinleistung und Wirkleistung sind gleich.
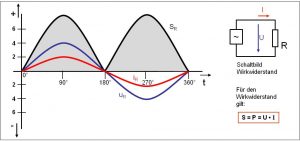
Errechnet man jetzt die Leistung durch Multiplikation von Strom und Spannung ergibt sich eine pulsierende positive Leistung (siehe Bild 1). Diese Leistung entspricht der Wirkleistung, die im Widerstand in Wärme umgesetzt wird.
Induktivität
Macht man den gleichen Versuch mit einer Spule (Induktivität), so zeigt sich eine Änderung im zeitlichen Verlauf von Strom und Spannung. Beide Sinuskurven sind um ca. 900 verschoben.
Bei einer Induktivität eilt der Strom der Spannung um 900 nach!
Sie erreichen nicht zum gleichen Zeitpunkt ihren Maximalwert und die Nulllinie. Ursache hierfür ist die Wechselwirkung zwischen Strom und Magnetismus, die das Induktionsgesetz beschreibt. Das durch den Stromfluss erzeugte und durch die Induktivität verstärkte Magnetfeld, erzeugt jetzt selbst einen „neuen“ Stromfluss. Dieser „induzierte Strom“ ist in seiner Richtung dem Strom entgegen gesetzt und behindert somit den Stromfluss durch die Spule.
Lenzsche Regel:
Der durch die Induktionsspannung hervorgerufene Strom ist stets so gerichtet, dass er der Ursache entgegenwirkt.
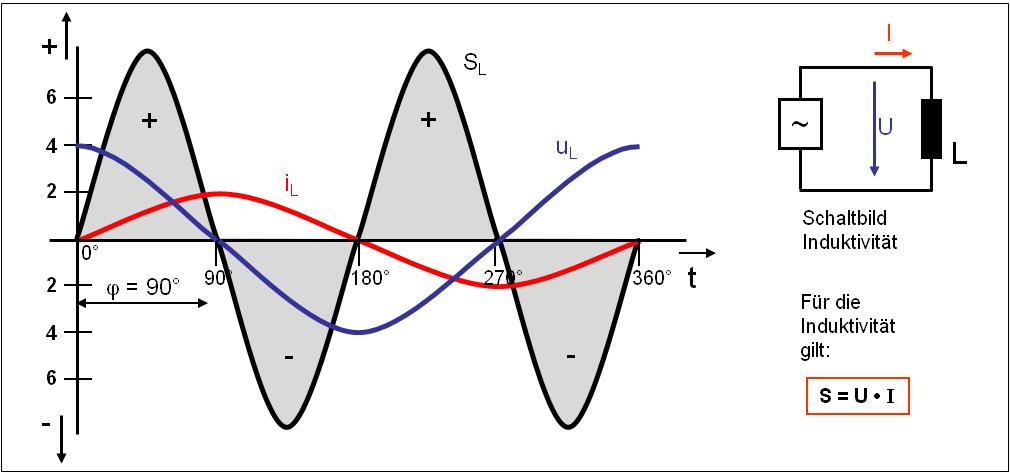
Errechnet man jetzt mit den gleichen Formeln wie beim Wirkwiderstand die Leistung durch Multiplikation von Strom und Spannung, ergibt sich ein ganz anderes Bild der Leistung (siehe Bild 2). Für eine fehlerfreie Berechnung ist der Zeitversatz zwischen Strom und Spannung zu berücksichtigen. Die Vorzeichen sind entsprechend den mathematischen Regeln einzusetzen. Die Leistung folgt somit einer Sinusschwingung. Die Leistung besteht aus positiven und negativen Anteilen. Die im Magnetfeld gespeicherte Energiemenge pendelt zwischen Spannungsquelle und Spule hin und her. Es wird, anders als beim Widerstand, keine Leistung in Wärme umgesetzt.
Klar, denn die Leistung (Energiemenge), die, die Spule zum Aufbau des Magnetfeldes benötigt (positive Halbwelle der Leistung) gibt sie ja wieder zurück, wenn das Magnetfeld zusammenbricht (negative Halbwelle der Leistung). Dieser Vorgang wiederholt sich bei jedem Nulldurchgang von Strom und Spannung.
Man kann sagen: Induktivitäten brauchen positive Blindleistung.
Zur Vereinfachung bei einfachen Berechnungen geht man von einer idealen Induktivität aus. Dies bedeutet, der ohmsche Widerstand der Drahtwicklung wird vernachlässigt bzw. mit 0 Ω angenommen. Für die meisten Berechnungen im Elektriker-Alltag ist dies völlig ausreichend, da der Blindwiderstand XL (Widerstand Magnetfeld) in der Regel wesentlich größer ist als der Wirkwiderstand R (Widerstand Drahtwicklung).
Kapazität
Macht man den gleichen Versuch mit einem Kondensator (Kapazität), so zeigt sich ebenfalls eine Änderung im zeitlichen Verlauf von Strom und Spannung. Beide Sinuskurven sind ebenfalls um ca. 900 verschoben, fast wie bei der Induktivität, aber diesmal in die andere Richtung.
Bei einer Kapazität eilt der Strom der Spannung um 900 voraus!
Sie erreichen nicht zum gleichen Zeitpunkt ihren Maximalwert und die Nulllinie. Ursache hierfür ist die physikalische Arbeitsweise des Kondensators. Zum Einschaltzeitpunkt ist der Kondensator noch ungeladen. Es fließt „viel Strom“ und die Spannung im Kondensator baut sich erst langsam auf.
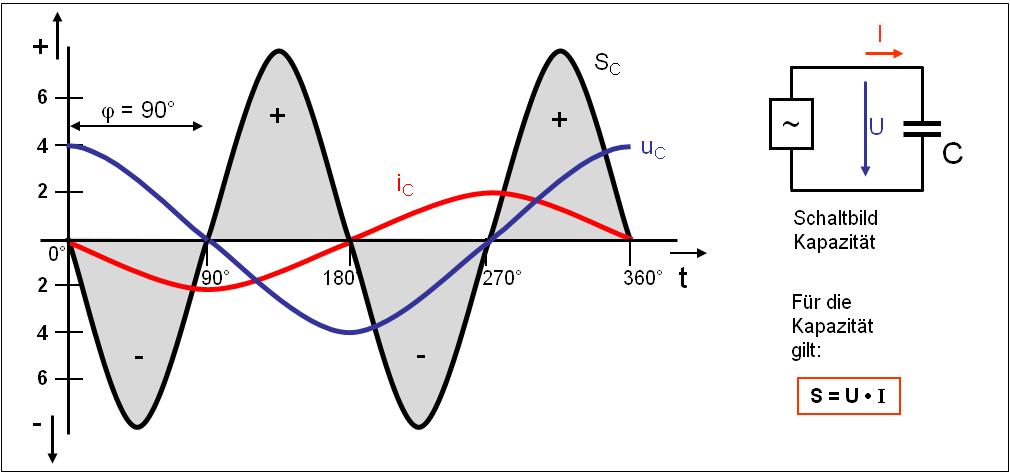
Errechnet man die Leistung durch Multiplikation von Strom und Spannung, ergibt sich das gleiche Bild der Leistung (siehe Bild 3) wie bei der Induktivität. Für eine fehlerfreie Berechnung ist der Zeitversatz zwischen Strom und Spannung zu berücksichtigen. Die Vorzeichen sind entsprechend den mathematischen Regeln einzusetzen. Die Leistung folgt einer Sinusschwingung. Die Leistung besteht aus positiven und negativen Anteilen. Die im Kondensator gespeicherte Energiemenge pendelt zwischen Spannungsquelle und Kondensator hin und her. Es wird keine Leistung in Wärme umgesetzt.
Klar, denn die Energiemenge, welche die Kapazität zum Aufladen benötigt (positive Halbwelle der Leistung) gibt sie ja beim Entladen wieder zurück (negative Halbwelle der Leistung). Dieser Vorgang wiederholt sich bei jedem Nulldurchgang von Strom und Spannung. Vergleicht man den Verlauf der Leistungskurve zwischen Induktivität und Kapazität, so ist zu erkennen, immer wenn die Leistungskurve bei der Induktivität im negativen Bereich ist, ist die Leistungskurve der Kapazität im positiven Bereich.
Prinzipiell sind die Verhältnisse bei der Kapazität umgekehrt wie die bei einer Induktivität.
Man kann sagen: Kapazitäten erzeugen positive Blindleistung.
Auch bei der Kapazität geht man zur Vereinfachung der Berechnungen von idealen Verhältnissen aus. Dies bedeutet, der ohmsche Widerstand der Drahtanschlüsse/Metallfläche wird vernachlässigt bzw. mit 0 Ω angenommen. Da der Blindwiderstand XC in der Regel wesentlich größer ist als der Wirkwiderstand R. Auch die Phasenverschiebung wird mit 900 gerechnet, obwohl dieser in der Realität eher etwas kleiner ist.
Zusammenfassung
Diese pendelnde Leistung wird als Blindleistung (Q in var – voltampere reaktiv) bezeichnet. Da sich die Leistung aus der Multiplikation von Spannung und Strom errechnet, werden diese als Blindspannung und Blindstrom bezeichnet. Für die Blindspannung und den –strom gibt es keine besonderen Formelbuchstaben, sie werden lediglich mit einem entsprechenden Index gekennzeichnet (z.B. UL, UC, IL, IC). Der Widerstand von Kapazitäten und Induktivitäten wird als Blindwiderstand (XL bzw. XC in Ω) bezeichnet.
Da die mathematischen Gesetzmäßigkeiten nach wie vor gelten, aber der zeitliche Versatz und das Vorhandensein dieser physikalischen Größen berücksichtigt werden muss, spricht man von „Blindanteilen“.
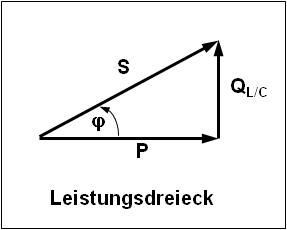
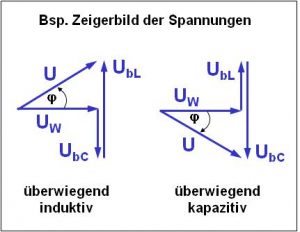
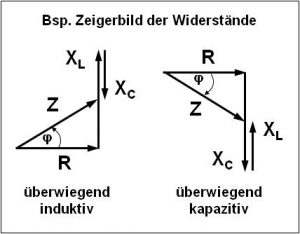
Das Zeigerbild der Leistungen zeigt den Zusammenhang zwischen der Wirkleistung P (in W), der Blindleistung Q (in var – induktiv oder kapazitiv) und der daraus resultierenden Gesamtleistung S (in VA – Voltampere) mit dem Phasenverschiebungswinkel φ. Der Leistungsfaktor bzw. Wirkleistungsfaktor cos phi (P/S) beschreibt, wie viel Wirkleistung in der Scheinleistung enthalten ist.
Zur Berechnung im rechtwinkligen Dreieck findet der Lehrsatz des Pythagoras (c2 = a2 + b2) oder die Winkelfunktionen (cos, sin, tan) Anwendung. Zur Berechnung der Gesamtleistung kann daher nur die geometrische Addition verwendet werden:
Da die Zuleitungen für elektrische Anlagen für die Gesamtleistung S dimensioniert sein müssen, lässt sich viel Geld und Material sparen, wenn die Blindanteile so klein wie möglich gehalten werden. Daher dürfen elektrische Anlagen bzw. Antriebe ab einer bestimmten Gesamtanschlussleistung von den EVU´s vorgeschriebene Grenzwerte für die Blindleistung nicht überschreiten. In diesem Falle werden dann Kompensationsanlagen zwingend notwendig.
Zu beachten ist auch, dass sich induktive und kapazitive Blindanteile gegenseitig aufheben – kompensieren. Bei der Berechnung wird der kleinere Blindanteil vom größeren abgezogen. Die folgende Auswahl einiger Zeigerbilder und Formeln verdeutlichen dies beispielhaft.
